Ordered list of fractions

 
The table below presents the first seventeen terms of an ordered list or index of fractions expressed in lowest terms.  The position of a fraction on the extended list can be determined without reference to prior terms of the list.  The following questions can be answered:

Given a fraction, what is its location on the Stern-Brocot (S-B) tree?
Given the k-th row on the Stern-Brocot tree, which fraction is the j-th term of that row (counting inclusively from the left)?

A

B

C

D

E

F

G

H

Decimal count

Binary count

Continued
fraction - convention explained below

Fraction

S-B tree:
row,
 term (counting inclusively from left)

If inequality is ‘>’ then fraction  is > 1

S-B tree term location 
calculated from
decimal count and
binary string length 

Decimal count 
calculated from
S-B location

1

1

1

1/1

1, 1

-

-

-

2

10

0; 1, 1

1/2

2, 1

1 = 2(2 - 1)/2

(22 – 2) / 2 = 1

22 - 2 (1) = 2

3

11

2

2/1

2, 2

2 > 2(2 - 1)/2

(3 + 1) / 2 = 2

2 (2) – 1 = 3

4

100

0; 1, 2

2/3

3, 2

2 = 2(3 - 1)/2

(23 – 4) / 2 = 2

23 - 2 (2) = 4

5

101

1; 1, 1

3/2

3, 3

3 > 2(3 - 1)/2

(5 + 1) / 2 = 3

2 (3) – 1 = 5

6

110

0; 2, 1

1/3

3, 1

1 < 2(3 - 1)/2

(23 – 6) / 2 = 1

23 - 2 (1) = 6

7

111

3

3/1

3, 4

4 > 2(3 - 1)/2

(7 + 1) / 2 = 4

2 (4) – 1 = 7

8

1000

0; 1, 3

3/4

4, 4

4 = 2(4 - 1)/2

(24 – 8) / 2 = 4

24 - 2 (4) = 8

9

1001

1; 2, 1

4/3

4, 5

5 > 2(4 - 1)/2

(9 + 1) / 2 = 5

2 (5) – 1 = 9

10

1010

0; 1, 1, 1, 1

3/5

4, 3

3 < 2(4 - 1)/2

(24 – 10) / 2 = 3

24 - 2 (3) = 10

11

1011

1; 1, 2

5/3

4, 6

6 > 2(4 - 1)/2

(11 + 1) / 2 = 6

2 (6) – 1 = 11

12

1100

0; 2, 2

2/5

4, 2

2 < 2(4 - 1)/2

(24 – 12) / 2 = 2

24 - 2 (2) = 12

13

1101

2; 1, 1

5/2

4, 7

7 > 2(4 - 1)/2

(13 + 1) / 2 = 7

2 (7) – 1 = 13

14

1110

0; 3, 1

1/4

4, 1

1 < 2(4 - 1)/2

(24 – 14) / 2 = 1

24 - 2 (1) = 14

15

1111
4

4/1

4, 8

8 > 2(4 - 1)/2

(15 + 1) / 2 = 8

2 (8) – 1 = 15

16

10000

0; 1, 4

4/5

5, 8

8 = 2(5 - 1)/2

(25 – 16) / 2 = 8

25 - 2 (8) = 16

17

10001

1; 3, 1

5/4

5, 9

9 > 2(5 - 1)/2

(17 + 1) / 2 = 9

2 (9) – 1 = 17

Examples

What is the location of \( \frac{19}{30} \) on the Stern Brocot tree?
  • The simple continued fraction of \( \frac{19}{30} \) is [0; 1, 1, 1, 2, 1, 2], by the Euclidean Algorithm.
  • The sum of the terms is 0 + 1 + 1 + 1 + 2 + 1 + 2 = 8. Therefore  \( \frac{19}{30} \) is on the 8th row of the Stern-Brocot tree, which has 2(8 - 1) =128 terms. (The n-th row of the Stern Brocot tree means the row containing \( \frac{1}{n} \))
  • The index binary number is 10100100, being 1's and 0's in alternating segments of length corresponding to the terms of the continued fraction.
  • The index decimal number is 4 + 32 + 128 = 164, being 10100100 expressed in decimal.  
  • By calculation in Column G for even index numbers: (28 - 164) / 2 = 46
  • The location of  \( \frac{19}{30} \) is in the 46th place (counting inclusively from left) in row 8, out of 27 =128 terms in total in row 8.
 What is the 301st term in row 10 of the Stern-Brocot tree?
  • From Column F,  2(10 - 1) / 2 = 256, being half the number of terms in the tenth row.  301 > 256, therefore the fraction sought is greater than 1. Its index number is odd. Fractions greater than 1 have an odd index number.
  • From Column H, using the equation for an odd index number, 2 (301) - 1 = 601. 601 is therefore the decimal index number of the fraction that is sought.
  • 601 in binary is 1001011001, being 512 + 64 + 16 + 8 + 1.
  • From Column C, the continued fraction that is sought is [1; 2, 1, 1, 2, 2, 1]
  • By calculating the continued fraction, the simplified fraction is \( \frac{61}{44} \), which is the 301st term (counting inclusively from the left) of row 10 of the Stern-Brocot tree out of 512 terms in total on row 10.
R Knott's online calculator lists all fractions < 1 to a given level of the Stern-Brocot tree. The calculator can be used to check the above results.  

Description of the index

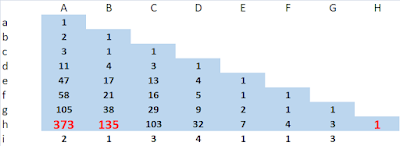
The index begins with the counting numbers in decimal (Column A). Each number is translated into binary form (Column B). The binary numbers encode a continued fraction based on the successive segments of terms containing alternately 1 and 0. For example, line 12 is twelve in binary, which is 1100, being two 1's followed by two 0's. The continued fraction is [0; 2, 2] (Column C). The resulting fraction is \( \frac{2}{5} \) (Column D).  

From a given fraction, the index number can be calculated via the simple continued fraction.  Every fraction has two simple continued fraction expressions.  By convention of this index, one of the two simple continued fraction expressions is used for a fraction with a value less than 1 and the other for its inverse.  Even index numbers (binary form ending in 0) refer to fractions less than one and odd index numbers (binary form ending in 1) refer to fractions greater than (or in one instance equal to) one.

Index numbers in binary form in column B provide some information about the location of terms on the Stern-Brocot tree.  The number of digits in a binary index expression is the same as the number of the Stern-Brocot row in which the corresponding fraction lives.  Index numbers that are even (ending in 0 in binary) refer to fractions less than 1 and odd index numbers refer to fractions greater than 1. 

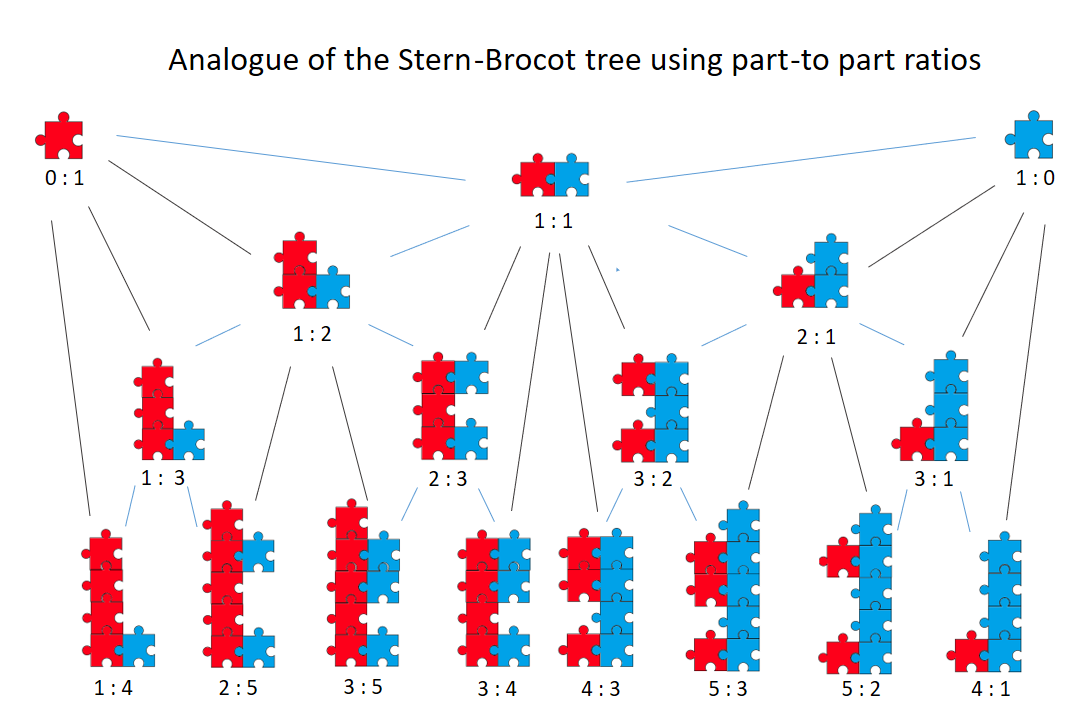
Column E lists the location of the indexed fractions on the Stern-Brocot tree by row and term.  Row 1 has one member,  \( \frac{1}{1} \); row 2 has two members,  \( \frac{1}{2} \) and  \( \frac{2}{1} \) and so on.  Terms are counted inclusively from the smallest value on the left of a row.  For example, the first term of the third row is  \( \frac{1}{3} \) and is expressed as (3, 1).

Column F is the first step in relating a known Stern-Brocot term to the index. Row R (R > 1) of the Stern-Brocot tree contains 2 (R - 1) terms of which half are smaller than 1 and half greater than 1.  If the position of a fraction \( \frac{p}{q} \) is further to the right than 2 (R - 1) / 2 terms, then  \( \frac{p}{q} \)> 1.  Otherwise  \( \frac{p}{q} \)  \( \leq \) 1.  This establishes the location of a term on the left (<1) or the right (>1) of the Stern-Brocot tree.

Column G calculates the location of a Stern-Brocot term from a known fraction via its index number.  The calculation differs, depending upon whether the index number is odd or even. The number of the Stern-Brocot row is deduced from the number of digits in the known index term expressed in binary.  For even numbers, the location of the Stern-Brocot term within the row (counting inclusively from the left) is given by  (2 (row number - index number) ) /2. For odd numbers, the location of the Stern-Brocot term is given by (index number + 1) / 2.  

Column H calculates an index number (and thence a fraction) from a known Stern-Brocot location.  Suppose that it is known only that some fraction is the j-th term on the k-th row of the Stern-Brocot tree.  From this information the value of that fraction can be calculated.  First, the calculation in column F establishes whether the fraction is greater or less than 1.  If the fraction is greater than one, its index number is given by 2k  - 2j . If the fraction is less than one, then its index number is given by 2j - 1.  In the latter case it is surprising that the calculation does not use the Stern-Brocot row number.  The reason for this is discussed below. From the index number the continued fraction and the fraction itself can be calculated. 

Patterns in the index

By convention in the design, an even index number refers to a fractions less than one and the following odd index number refers to its inverse.  

The index is grouped in order of rows of the Stern-Brocot tree.  For example, the index binary numbers 1000, 1001,... up to 1111 all refer to fractions in the fourth row of the tree.  Fractions [a1, a2, ..., ak] in the same row of the tree have the same sum of terms of their continued fractions: a1 + a2 + ... + ak.  The length of a binary string determines the terms of the continued fraction.  So a string of length k will refer to a fraction whose terms sum to k and which is located after k right or left moves down the tree.  Cut the Knot presents another approach to indexing which uses the same observation.

In this index all binary encodings begin with a '1'.  The longer the first string length of '1's, the higher the value of the first non-zero term of the corresponding continued fraction.  For example, considering even numbers, 1000 represents [0;1,3] and 1100 represents [0;2,2];  the odd-number neighbours are respectively 1001 which represents [1; 3] and 1101 which represents [2; 2].  As even numbers increase - beginning with longer strings of '1's  - and as the value of the first continued fraction term also increases, then the value of the continued fraction decreases.  In this way the index encodes fractions less than one in decreasing order, row by row.  Their inverses are encoded in increasing order.  The pattern of index numbers in relation to the Stern Brocot tree is illustrated here below:


Validating the methods

No formal proofs are given here.  Most of the arguments needed for formal proofs are given.

The questions addressed here are;
  1. Completeness of the index.  Does the index capture all simplified fractions?
  2. Parsimony of the index.  Does the index capture only simplified fractions?
  3. Uniqueness of reference.  Does each term of the index refer to exactly one fraction and vice-versa?
  4. Mapping to and from the Stern-Brocot tree.  Does the index generate valid references to the Stern-Brocot tree and vice versa?
There are two main problems with encoding continued fractions by using binary segments of lengths corresponding to the sequence of numbers in the continued fraction.

The first problem concerns the encoding of the whole number preceding the ';' in, for example, [1; 1, 2, 2]. This fraction could be encoded as 101100. The question then arises, how to encode the continued fraction [0; 1, 1, 2, 2]. This continued fraction begins with '0' and by the encoding rule the part preceding the ';' would be represented by a binary segment of zero length, which would not give any information.

The second problem concerns the fact that every fraction has two continued fraction expressions. The expression [1; 1, 2, 2] refers to the same fraction as does [1; 1, 2, 1, 1], namely \( \frac{12}{7} \). The binary representations would be: of the first 101100 and of the second 101101. In that way there would be two different encodings of the same fraction. The index would not refer uniquely.

In the example in the last paragraph the continued fraction is encoded as two consecutive binary numbers: 101100 plus 1 equals 101101. This is not a co-incidence.

These two problems are solved together by a convention in the index:

If the binary representation is even (ends in 0), then that binary number represents a fraction less than 1.
If the binary representation is odd (ends in 1), then that binary number represents a fraction that is greater than 1.



_____________________________________________


\( \frac{1}{p+\frac{1}{q +\frac{1}{r}}} \)

\( \frac{1}{p+\frac{1}{q +\frac{1}{r+\frac{1}{s+\frac{1}{t+\frac{1}{u+\frac{1}{v+\frac{1}{w}}}}}}}} \)


Comments

Post a Comment

Popular posts from this blog

Counting fractions

Given a list of fractions, I am looking for a way to identify the n th member of the list without needing to work out all the fractions before the n th one.  Also, given any fraction, I want to be able to say where it appears on the list. I am looking for reduced fractions, which means that  \( \frac{1}{2} \) will appear in my list but I will not see  \( \frac{2}{4} \), \( \frac{3}{6} \) or any others that can be reduced to simpler terms. There are methods to create lists of reduced fractions. In particular: The Stern-Brocot tree.  The Calkin Wilf sequence.  Kepler's method in Harmonices Mundi.  There are methods to locate fractions in these sequences.  Bates, Bunder and Tognetti   presented a method in 2010.   Cut the Knot also discussed binary encoding as a means of locating fractions.  A page on this blog proposes a method that is reasonably simple and intuitive and that yields insight into the structure of fractions.
Read more

Continued Fraction Triangle

Image
This post is about patterns in the calculation of a continued fraction and its reverse and in successive  truncations of a continued fraction. Table 1: calculation of continued fraction (row i) from integers 373 and 135 (row h) and calculation of convergents by successively truncating the continued fraction (upwards, rows g to a).  Column H row h is the greatest common divisor of 373 and 135. Table 2:  reverse continued fraction from Table 1 with successive convergents. DESCRIPTION OF TABLES 1 AND 2 Table 1 is a calculation of continued fraction (row i) from integers 373 and 135 (row h) and calculation of convergents by successively truncating the continued fraction by one term at a time (working upwards, rows g to a).  Column H row i is the greatest common divisor of 373 and 135.  The continued fraction can be interpreted as either [2; 1, 3, 4, 1, 1, 3], which represents  \( \frac{373}{135} \) or [0; 2, 1, 3, 4, 1, 1, 3], which is the inverse \( \frac{135}{373} \). Row g of Table 1 ca
Read more

Stern-Brocot Tree and Ratios

Image
  Captions refer to the part-to-part ratio of blue to red units. A jigsaw group of units is made by copying, from the row above it, the two groups between which it will sit (reading left to right) and then by joining them together.   This operation is analogous to calculating the mediant of two fractions by adding numerators and adding denominators. The two u pward lines from each group of units lead to its two ‘parent’ groups and darker lines lead to the more distant of the two parents.  The Stern-Brocot tree generates simple fractions.   The aim is to show that the structure of the Stern-Brocot tree can be reproduced by repeated addition of units without reference to fractions.   In this way the concept ‘one divided by zero’ is obviated in the first row. Achille Brocot was a watch-maker and the Stern-Brocot tree originated in the problem of how to find the best approximations to ideal gear ratios that were too big to manufacture.  Hayes, 2000    In a similar way, the Calkin Wilf tr
Read more