Adapted Euclidean Algorithm

 HEADLINE CONTENT

A                    31 (1)  -  13 (0)   =   31    First chosen starting number 

B                    31 (0)  -  13 (1)   =  -13    Second chosen starting number multiplied by -1

C = A + B      31 (1)  -  13 (1)    =  18    Add the smallest positive result obtained so far to the smallest negative result so far

D = B + C      31 (1)  -  13 (2)    =   5     Repeat the above operation: add smallest negative to smallest positive and write as the next member of the list

E = B + D      31 (1)  -  13 (3)    =  -8     

F = D + E      31 (2)  -  13 (5)    =   -3     

G = D + F      31 (3)  -  13 (7)    =   2

H = F + G      31 (5)  -  13 (12)  =  -1

I = G + H       31 (8)  -  13 (19)  =   1

J = H + I        31 (13) - 13 (31)  =   0

'Smallest negative' means 'closest to zero', i.e. lowest absolute value. The list of equations above yields in a single process a number of results about the fraction \( \frac{13}{31} \).  An introduction and explanation are given on this page.

FULL CONTENT

On this page the Euclidean algorithm and extended Euclidean algorithm are adapted and combined to create a single algorithm which will yield:

• the greatest common divisor of two whole numbers, a and b
• a / b in reduced form
• the lowest values x and y such that ax + by = gcd (a,b) (Bézout identity)
• successive 'best' approximations to the fraction a / b by showing the 'route' to the fraction a / b along branches of the Stern-Brocot tree
• the simple continued fraction equal to a / b
• a series of unit fractions adding to a / b ('Egyptian fraction')

This is not a new invention, although I have not seen it presented elsewhere in a way that produces the above results by means of a single process.  The right hand side of the equations is also known as the subtractive Euclidean algorithm. The method seems to be essentially the same as the method in W. Dubuque's answer and link here.   I believe that there are many other references. In these notes the links to the Stern-Brocot tree, successive approximations, and simple continued fractions are highlighted.  Any mistakes are mine.

STAGE 1 - BUILDING THE ALGORITHM

The first stage deals with one side of a set of equations that are generated by the algorithm. Take two different counting numbers.  Multiply one of the numbers by -1 so that one number is positive and the other is negative: a, -b.  Start a list, beginning with a and -b.  Add them: a + (-b) = a - b and add this result to the list. If the result is positive, add it to the negative number and write the result as the next member of the list. If the result is negative, add it to the positive number and add the result to the list. Repeat, each time adding the smallest positive number thus far to the ‘smallest’ (closest-to-zero) negative number thus far and writing the new result as the next member of list. The ‘span’ (absolute difference) between the smallest positive and smallest negative terms will shrink to the point that it is defined by the positive and the negative greatest common divisor of a and b, which then add to zero.  (Why?  In short, this works for the same reasons that the Euclidean algorithm produces the greatest common divisor (gcd) of two numbers and then proceeds to zero.  This method is also known as the subtractive Euclidean algorithm.)

Example:  

Let the starting numbers be 31, 13.  The resulting sequence is:   31;  -13;  18;   5;   -8;   -3;   2;   -1;   1;   0.

The calculations giving rise to the sequence are:

                31     Starting number 31

               -13     Starting number 13 multiplied by -1

                

31 - 13 = 18     31 is smallest positive in the list and -13 is smallest (closest-to-zero) negative: add 31 and -13

18 - 13 =  5     18 is smallest positive so far; add to smallest negative so far, which is -13 

  5 - 13 = -8      5 is smallest positive so far; add to smallest negative so far, which is -13    

  5 -  8  = -3     -8 is smallest negative so far; add to smallest positive so far, which is 5  

  5 -  3  =  2      5 is smallest positive so far; add to smallest negative so far, which is -3  

  2 -  3  = -1      2 is smallest positive so far; add to smallest negative so far, which is -3  

  2 -  1  =  1      2 is smallest positive so far; add to smallest negative so far, which is -1  

  1 -  1  =  0      1 and -1 are the smallest positive and negative numbers and add to 0

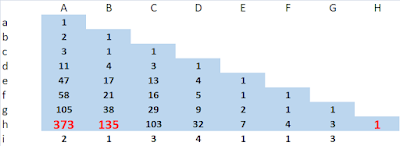
The illustration below shows how the algorithm 'squeezes' the starting numbers together around zero.  Similarly to the Euclidean algorithm, the results have the same greatest common divisor as the starting numbers.  Suppose gcd(31,13) is x.  Then 31 = ax and 13 = bx.  Then 31 - 13 = 18 = ax - bx = x(a-b). So 18 is divisible by x, which is gcd(31,13).  Each line is composed of prior terms generated in the same way. So gcd(31,13) is preserved throughout the results.  

Figure 1: Example of the algorithm as applied to 31 and 13. The algorithm produces an ever narrower 'span' that includes zero.

 

In general:

Let a and -b be the starting numbers. If a - b is a negative number, then add it to the smallest positive number, which is a.  The result is 2a - b. If a - b is a positive number, then add it to the 'smallest' negative number, which is -b.  The result is a - 2b.  Suppose for some pair of starting numbers  that a - b is positive - that is, a > b in absolute terms - and the result so far is (a - b) + (-b) = a - 2b .  We now work with a - 2b.  If a - 2b positive, add to the smallest negative number thus far, which is -b.  The result is a - 3b.  If a - 2b is negative, add to the smallest positive number thus far, which is a - b.  The result is 2a - 3b.  The process continues, each time adding the 'smallest' negative number thus far to the smallest positive number thus far.  (In these notes, 'smallest' always means 'closest-to-zero'.)

STAGE 2 - STRUCTURE OF THE ALGORITHM

The possible 'routes' that the algorithm will take may be represented as a tree.  Each term beyond the starting numbers is a node in the tree and each node has two off-shoots, one for the case in which that term is positive and one for the case in which it is negative. The route will be completely determined by the value of the starting numbers and each route will be unique for any coprime pair of starting numbers. 

Figure 2: the 'adapted Euclidean algorithm' tree. The first and second levels are given by the starting numbers.  To calculate the third level we need to know whether (a - b)  is a positive or negative number.  The options are shown by the + and - signs just below the (a - b) term in Figure 2.  If (a - b ) represents a positive number, then it is the smallest positive number so far in the process and so it should be added to the smallest (closest to zero) negative number, which is -b.  The result is a - 2b.  On the other hand, if (a - b) is negative, then it is the 'smallest' negative number so far and so should be added to the smallest positive term so far, which is a.  The result in this case is 2a - b. 

From each term in the tree two options arise: one for the case in which it is positive and one for the case in which it is negative.  The choice is determined by the particular starting numbers: for example, if a is much larger than -b in absolute terms, then the route down the tree will continue on the left hand side further, traversing (a - 2b) then (a - 3b), (a - 4b) etc., until a coefficient k is reached such that kb > a, at which point the route would switch to a 'negative' direction and proceed to the gcd (a,b) and then to zero as in Figure 1.

To calculate the next level beyond the bottom of the diagram, select a term from the lowest level shown, e.g. 5a - 3b.  Now assume that 5a - 3b is a positive number.  In that case, we trace the route up the tree from 5a - 3b until we find a negative term.  The first negative term we find must be the smallest (closest-to-zero) negative term thus far, because the 'span' between terms in the sequence ending in 5a - 3b will always become smaller for any starting numbers (Figure 1).  In this case, the first negative term we find is just one level above and it is 3a - 2b.  So, if 5a - 3b is positive, then its offshoot will be (5a - 3b) + (3a - 2b) = 8a - 5b.  On the other hand, assume that 5a - 3b represents a negative number.  Again, trace the route up the tree until we find the first positive term, which will be the smallest positive term so far.  The route in this case goes first to (3a - 2b), which is negative and therefore not the term we need; and then to 2a - b, which is positive and is the term we need.  So, if 5a - 3b is negative, then its offshoot will be (5a - 3b) + (2a - b) = 7a - 4b.

Operating the algorithm in a particular case is simpler than showing the options in general terms.  In the particular case, we are only dealing with one route down the tree.

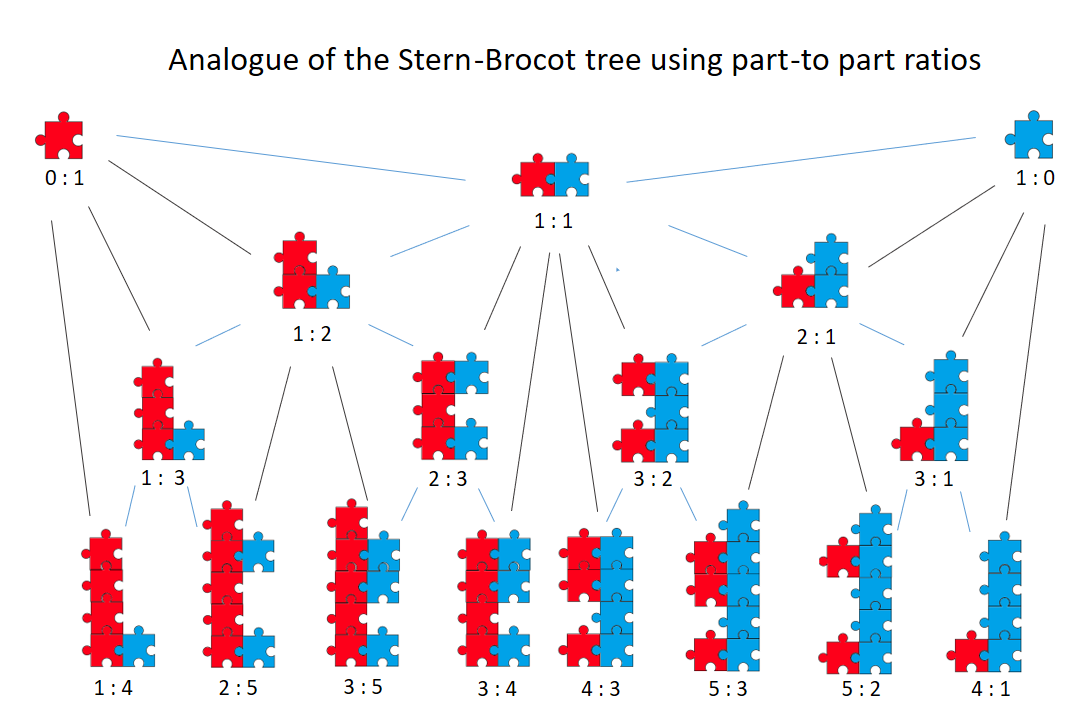
Note the pattern of coefficients of a and b as they appear in the tree.  They are the numbers representing the numerators and denominators of fractions in the Stern-Brocot tree.  Until now, I have not mentioned fractions in this exercise, which has dealt only with whole numbers and with addition and subtraction.  To explain this parallel I will present the 'adapted Euclidean algorithm' with more information. 

STAGE 3 - COMPLETING THE ALGORITHM

So far I have focussed only on the right hand side of equations in the algorithm. I shall now expand the algorithm by including the coefficients of the two starting numbers at each step.  I use an example to show how the algorithm can be applied.  This will provide information about the ratio between the two starting numbers. A general formulation of the algorithm is given at Stage 4.  Taking the same example as above:

A                    31 (1)  -  13 (0)   =   31    First chosen starting number 

B                    31 (0)  -  13 (1)   =  -13    Second chosen starting number multiplied by -1

C = A + B      31 (1)  -  13 (1)    =  18    Add the smallest positive result obtained so far to the smallest negative result so far

D = B + C      31 (1)  -  13 (2)    =   5     Repeat the above operation: add smallest negative to smallest positive and write as the next member of the list

E = B + D      31 (1)  -  13 (3)    =  -8     

F = D + E      31 (2)  -  13 (5)    =   -3     

G = D + F      31 (3)  -  13 (7)    =   2

H = F + G      31 (5)  -  13 (12)  =  -1

I = G + H       31 (8)  -  13 (19)  =   1

J = H + I        31 (13) - 13 (31)  =   0

Each line of the algorithm is determined by the results previously obtained on the right hand side of the equations, as at Stage 1 above. On the right hand side, the 'smallest' (closest-to-zero) negative number on the list so far is added to the smallest positive number; and on the left side the equations that result in those two numbers are added by adding the coefficients of the starting numbers.  

The pairs of coefficients in the algorithm as applied to 31 and 13 correspond to the coefficients in the algorithm tree illustrated in Figure 2 above as far as 2a - 5b.  The route down the algorithm tree in this case is (a-b), (a-2b), (a-3b), (2a-5b), and so on, according to the coefficients in the equations listed above.  

Analogue to the Stern-Brocot tree

When I add two equations in the algorithm, I am adding the coefficients of two constant numbers, which are the starting numbers.  If I consider the coefficients as numerators and denominators of fractions, then this is equivalent to calculating the mediant of two fractions by adding numerators and adding denominators.  For example, the mediant of  \( \frac{2}{5} \) in line F and \( \frac{3}{7} \) in line G is \( \frac{2+3}{5+7} \) in line H, that is, \( \frac{5}{12} \).

The coefficients of the starting numbers in lines A and B correspond to the zero-th line of the Stern-Brocot tree, in which  \( \frac{0}{1} \) represents 0 and  \( \frac{1}{0} \) represents a boundless reservoir of positive rational numbers.  The coefficients in line C are identical for any starting numbers.  Line C represents the operation of calculating the mediant of  \( \frac{0}{1} \) and  \( \frac{1}{0} \), which is \( \frac{1}{1} \).  In terms of the algorithm, line C is calculating the difference between the two starting numbers.  It tells us that the starting numbers are in some finite ratio, of which the first approximation is 1:1.

To obtain line D, I add the coefficients of lines B and C.  Lines B and C are selected because they are the equations with smallest positive and smallest (closest-to-zero) negative results. This is equivalent to calculating the mediant of two fractions as described two paragraphs above.  It is also equivalent to calculating a particular route down the Stern-Brocot tree by matrix multiplication:

The columns of the first matrix represent the coefficients 0, 1 in line B and 1, 1 in line C. The right hand column of the third matrix is the sum of the two columns of the first matrix; the left hand column remains unchanged.  The second matrix is the operator to achieve this result.  It is an instruction to move down the Stern Brocot tree one row and to the left.  

Cross-multiplying coefficients of two neighbouring lines in the adapted algorithm results in |1|, e.g. from lines F and G:  2 x 7 - 3 x 5 = -1 and 3 x 12 - 5 x 7 = 1.  This is expected, because the determinant of the initial matrix is 1 and each matrix (that is, the coefficients in two neighbouring lines) is obtained by multiplying a previous matrix by an operator matrix with determinant |1|. 

The above shows that the adapted algorithm is equivalent to finding the fraction represented by the two starting numbers as numerator and denominator on the Stern-Brocot tree.  The route ending at \( \frac{13}{31} \)  is  \( \frac{1}{1} \),\( \frac{1}{2} \), \( \frac{1}{3} \), \( \frac{2}{5} \), \( \frac{3}{7} \), \( \frac{5}{12} \), \( \frac{8}{19} \), \( \frac{13}{31} \).

Greatest Common Divisor and Bézout identity 
Similarly to the Euclidean algorithm, the absolute value of the penultimate result (line I)  is the greatest common divisor of the starting numbers.  There are two lines whose absolute values are gcd(31,13): one is positive and one is negative (lines H and I), as illustrated in Figure 1 above.  The coefficients on the left hand side of lines H and I represent the two 'parent' fractions on the Stern-Brocot tree of the fraction represented by the two starting numbers.  That is,  \( \frac{13}{31} \) (line J) is the mediant of  \( \frac{8}{19} \) (line I) and \( \frac{5}{12} \) (line H). For some starting numbers the negative result will occur in the penultimate line and the equations representing the gcd may not be on adjacent lines.  For any starting numbers, there will be two members of the list of opposite sign and equal absolute value and the equation related to the one of the terms is the Bézout identity with lowest coefficients .

Successive approximations

When the right hand side of the equation is negative, then the fraction represented by the coefficients on the left hand side is less than the fraction represented by the two starting numbers.  This can be seen by setting up the equation as fractions and cross-multiplying, which is the same calculation as the original equation.  For example: 

Line F    31 (2)  -  13 (5)    =   -3  ;  therefore \( \frac{2}{5} \) <  \( \frac{13}{31} \)

In the same way, when the right hand result is positive, then the fraction represented by the coefficients on the left hand side is greater than the fraction represented by the two starting numbers. The results on the right hand side are in descending (getting closer to zero) order of positive and negative numbers.  These numbers represent the numerators of the difference between the fraction represented by the starting numbers and the fraction represented by the coefficients .  The denominators of the difference between the two fractions are represented by the product of one coefficient and one starting number.  The coefficients always increase, because the equations are successively added.  Numerators decrease and denominators increase as the list grows: therefore, given any approximation in the list, the next approximation bearing the same sign will be closer to the starting numbers' fraction than the previous approximation.   

Figure 3.  Successive approximations to \( \frac{13}{31} \)  resulting from the adapted algorithm.  These are 'best' approximations in the sense that there are no fractions with smaller denominators that are closer to \( \frac{13}{31} \). This is a feature of the Stern-Brocot tree. The algorithm generates the 'route' down the Stern-Brocot tree.

The continued fraction

In the Euclidean algorithm, the simple continued fraction of the starting numbers is deduced from the coefficients that are generated at each step.  In the adapted algorithm, the continued fraction is deduced from the pattern of negative and positive signs of the results of each equation.   The sequence of results is 31;  -13;  18;   5;   -8;   -3;   2;   -1;   1;   0.  The first two terms set up the algorithm and represent the fraction whose continued fraction I am calculating.  Counting from the third term inclusive, there are two positive terms, two negative, one positive, one negative, one positive and finally zero.  This represents the continued fraction [0; 2, 2, 1, 1, 2] which is  \( \frac{13}{31} \).  The last number in the continued fraction is 2 because the final zero of the algorithm is counted as having the same sign as the penultimate term.  A continued fraction represents a route down the Stern-Brocot tree, to which the adapted algorithm is analogous.  As seen above, we can also generate \( \frac{13}{31} \) by successive matrix multiplication for the required number of steps to 'left' and 'right' in the Stern Brocot tree; this will in turn generate the coefficients for the equations in the adapted algorithm.

Starting numbers that are not coprime

The coefficients of the final equation (line J above) with result 0 represent the reduced fraction of the starting numbers.  In the example above, the starting numbers are coprime and so the reduced fraction is the same as the original fraction.  For an example of non-coprime starting numbers, consider 26 and 16:

A'                     26 (1)  -  16 (0)   =   26    First chosen starting number 

B'                     26 (0)  -  16 (1)   =  -16    Second chosen starting number multiplied by -1

C' = A' + B'      26 (1)  -  16 (1)    =  10    Add smallest positive result to the smallest negative result so far and write as the next member of the list

D' = B' + C'      26 (1)  -  16 (2)    =  -6     Repeat the above operation: add smallest negative to smallest positive

E' = C' + D'      26 (2)  -  16 (3)    =   4     

F' = D' + E'      26 (3)  -  16 (5)    =   -2     

G' = E' + F'      26 (5)  -  16 (8)    =   2

H' = F' + G'      26 (8)  -  16 (13)  =   0

In the above example the coefficients of the final line H' are 8 and 13 and the result is 0 because \( \frac{8}{13} \) = \( \frac{16}{26} \).  That is, \( \frac{8}{13} \) is \( \frac{16}{26} \) in reduced form.
Lines F' and G' have results of the same absolute value, 2,  and are of opposite signs. Therefore 2 is the gcd(26,16). 
The Bézout identity equations are derived from lines G' and F' because the 2 is the gcd(26,16):         
26 x 5 - 16 x 8 =  16 x 5 - 26 x 3 =  2 = gcd(26,16)
The continued fraction is deduced from the changes in signs of the results of each line and is [0; 1, 1, 1, 1, 2], which is  \( \frac{8}{13} \).  

STAGE 4 - DIVISION

Up to this stage I have used only addition and subtraction.  This limitation brings out the structure of the algorithm and reveals each step in the Stern-Brocot tree ending in the ratio of the starting numbers. The algorithm can incorporate division, which shortens the process.  It is equivalent to using matrix multiplication using

for left and right moves respectively down branches of the Stern-Brocot tree, where k represents the absolute floor value of the division of the larger by the smaller of the two smallest results of opposite signs so far obtained.

LINE INDEX	INSTRUCTION	CALCULATION	ALGORITHM LIST
A	Set up first equation with a starting number and make it the first entry in a list	a (1) - b (0) =  a	a (1) - b (0) =  a
B	Set up second equation with starting number and enter in the list	a (0) - b (1) = -b	a (0) - b (1) = -b
C	Select from the list the equation with smallest positive result (at first iteration this is a)	a (q1) - b (q2) =  n1
D	Select from the list the equation with smallest (closest-to-zero) negative result (at first iteration this is -b)	a (q3) - b (q4) =  -n2
E	Let n1 >  abs ( n2) without loss of generality. Calculate absolute value of floor of abs (n1 / n2.)	Floor abs (n1 / n2) = K1
F	Multiply equation D by E	a (q3 K1) - b (q4 K1) = - n2 K1
G	Add F to C (still assuming n1 > n2) and enter in list	a (q1 + q3 K1) - b (q2 + q4 K1) = n1 - n2 K1	a (q1 + q3 K1) - b (q2 + q4 K1) = n1 - n2 K1
H	Repeat from line C

The term highlighted in red is the first term in the continued fraction.  For example:

LINE INDEX	INSTRUCTION	EXAMPLE: CALCULATION	EXAMPLE: ALGORITHM LIST
A	Set up first equation with starting number and make it the first entry in a list	17 (1) - 5 (0) = 17	17 (1) - 5 (0) = 17
B	Set up second equation with starting number and enter in the list	17 (0) - 5 (1) = -5	17 (0) - 5 (1) = -5
C	Select from the list the equation with smallest positive result	17 (1) - 5 (0) = 17
D	Select from the list the equation with smallest (closest-to-zero) negative result.	17 (0) - 5 (1) = -5
E	Calculate absolute value of floor of C and D (17 / -5)	Floor (17 / 5) = 3
F	Multiply equation D by E	17 (0 x 3) - 5 (1 x 3)  = 3 x -5 17 (0) - 5 (3) = -15
G	Add F to C and enter in list	17 (0 + 1) - 5 (3 + 0) = 2	17 (1) - 5 (3) = 2
H	Repeat from line C
I	Smallest positive result so far = G	17 (1) - 5 (3) = 2
J	'Smallest' (closest to zero) negative result so far = B	17 (0) - 5 (1) = -5
K	Floor value J, I	Floor (5 / 2) = 2
L	Product I,K	17 (1 x 2) - 5 (3 x 2) = 2 x 2
M	Sum J, L and enter in list	17 (0 + 2) - 5 (1 + 6) = -1	17 (2) - 5 (7) = -1
N	Smallest positive result so far = G	17 (1) - 5 (3) = 2
O	Smallest negative result so far = M	17 (2) - 5 (7) = -1
P	Floor value N,O	Floor (2 / 1) = 2
Q	Product P, O	17 (4) - 5 (14) = -2
R	Sum N, Q	17 (1 + 4) - 5 (3 + 14) = 0	17 (5) - 5 (17) = 0

The figures highlighted in red represent the number of left or right moves down the branches of the Stern-Brocot tree before the direction changes.  They are thus the terms in the continued fraction formed by the starting numbers.  In this case, the continued fraction of  \( \frac{5}{17} \) is [0; 3, 2, 2].

The term highlighted in blue represent one Bézout identity. Similarly to the Euclidean algorithm, the absolute value of the penultimate term is the greatest common divisor of the starting numbers.

SUMMARY
The adapted algorithm presented on this page combines the work of several other processes.  The Euclidean algorithm establishes the greatest common divisor of two numbers and the simple continued fraction associated with their ratio.  The reduced fraction associated with the starting numbers can be calculated separately when the greatest common divisor is known. The extended Euclidean algorithm provides the Bézout identity.  Matrix multiplication, using terms from the continued fraction, defines the route along the Stern Brocot tree to the fraction represented by the starting numbers and provides a list of 'best' approximations to that fraction; it also establishes the two 'parent' fractions of which the starting number fraction is the mediant 'child'. The adapted algorithm presented on this page provides the highlighted information by a unified process that is simple to operate.

A                    31 (1)  -  13 (0)   =   31    First chosen starting number 

B                    31 (0)  -  13 (1)   =  -13    Second chosen starting number multiplied by -1

C = A + B      31 (1)  -  13 (1)    =  18    Add the smallest positive result obtained so far to the smallest negative result so far

D = B + C      31 (1)  -  13 (2)    =   5     Repeat the above operation: add smallest negative to smallest positive and write as the next member of the list

E = B + D      31 (1)  -  13 (3)    =  -8     

F = D + E      31 (2)  -  13 (5)    =   -3     

G = D + F      31 (3)  -  13 (7)    =   2

H = F + G      31 (5)  -  13 (12)  =  -1

I = G + H       31 (8)  -  13 (19)  =   1

J = H + I        31 (13) - 13 (31)  =   0

POST SCRIPT

UNIT FRACTION SUM ('EGYPTIAN FRACTION')

Δοσ μοι που στω και κινω την γην