Continued Fraction Triangle

This post is about patterns in the calculation of a continued fraction and its reverse and in successive 
truncations of a continued fraction.

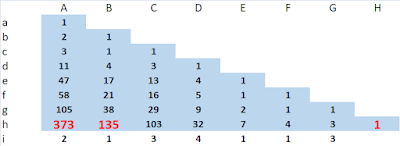
Table 1: calculation of continued fraction (row i) from integers 373 and 135 (row h) and calculation of convergents by successively truncating the continued fraction (upwards, rows g to a).  Column H row h is the greatest common divisor of 373 and 135.

Table 2:  reverse continued fraction from Table 1 with successive convergents.

DESCRIPTION OF TABLES 1 AND 2

Table 1 is a calculation of continued fraction (row i) from integers 373 and 135 (row h) and calculation of convergents by successively truncating the continued fraction by one term at a time (working upwards, rows g to a).  Column H row i is the greatest common divisor of 373 and 135.  The continued fraction can be interpreted as either [2; 1, 3, 4, 1, 1, 3], which represents  \( \frac{373}{135} \) or [0; 2, 1, 3, 4, 1, 1, 3], which is the inverse \( \frac{135}{373} \).

Row g of Table 1 calculates the same continued fraction but without its final term.  The resulting integers (105 and 38) represent the co-efficients of a Bézout identity for 373 and 135.  That is to say: 38 x 373 - 105 x 135 = |1|.   Each two-by-two array within the blue highlighted triangle also cross-multiplies to |1|.  Columns A and B contain successive convergents to the fraction created by 373 and 135. The reason for this is discussed below.

Table 2 begins in row i with the reversal of the continued fraction from Table 1.  Table 2 is completed by successive truncation of the reversed continued fraction.  The number 373 appears in the same place in Tables 1 and 2, representing the fact that the numerator of a continued fraction is the same as the numerator of its reversal.  As in Table 1, each two-by-two array within the blue highlighted triange cross-multiplies to 1.  

The blue-highlighted sections of Tables 1 and 2 are mirror images of each other, the line of reflection being the upward sloping diagonal from column A row h to column D row d containing the numbers  373, 38, 16 and 4.

CALCULATION METHOD AND MATERIALS FOR PROOFS

Rows i and h are calculated from the chosen integers 373 and 105 in Table 1 and Table 2 above as follows:

Euclidean algorithm	A = k B + r	B =  k1 r + r1	r = k2 r1 + r2	r1 = k3 r2 + g	r2 = k4g + 0	gcd (A,B) = g
Continued fraction	k	k1	k2	k3	k4

Table 3:  calculation method for rows h and i in Tables 1 and 2, showing application of the Euclidean algorithm

Row g in Tables 1 and 2 is calculated by truncating the final term of the continued fraction in row i.  Rows f to a, working upwards, truncate the continued fraction successively one term at a time, as below:

Calculation of continued fraction truncated at penultimate term (right to left)	k k1k2 k3 + k k1 + k k3 + k2 k3 + 1	k1k2 k3 + k1 + k3	k2 k3 + 1	k3	1
Euclidean algorithm	A = k B + r	B =  k1 r + r1	r = k2 r1 + r2	r1 = k3 r2 + g	r2 = k4g + 0	gcd (A,B) = g
Continued fraction denominators	k	k1	k2	k3	k4

Table 4:  calculation method for row h in Tables 1 and 2, showing truncation of the continued fraction in row i

Continued fraction and reversal: how they are related

Tables 5a and 5b below illustrate the relationship between a continued fraction and its reversal and between the two fractions represented by them, as follows:

Calculation of continued fraction truncated at penultimate term (right to left)	C = k k1k2 k3 + k k1 + k k3 + k2 k3 + 1	D = k1k2 k3 + k1 + k3	k2 k3 + 1	k3	1
Calculation of continued fraction (right to left)	A = k k1k2 k3 k4 + k k1 k2 + k k1 k4 + k k3 k4 + k + k2 k3 k4 + k2 + k4	B = k1 k2 k3 k4 + k1 k2 + k1 k4 + k3 k4 + 1	k2 k3 k4 + k2 + k4	k3 k4 + 1	k4	gcd (A,B) = 1
Denominators of continued fraction	k	k1	k2	k3	k4

Table 5a:  expanded calculation of continued fraction and the same continued fraction truncated by one term.

Calculation of reverse continued fraction truncated at penultimate term (right to left)	B = k1 k2 k3 k4 + k3 k4 + k1 k4 + k1 k2 + 1	D = k1k2 k3 + k3 + k1	k1 k2 + 1	k1	1
Calculation of reversed continued fraction (right to left)	A = k k1k2 k3 k4 + k2 k3 k4 + k k3 k4  + k k1 k4 + k4 + k k1 k2 + k2 + k	C = k k1 k2 k3 + k2 k3 + k k3 + k k1 + 1	k k1 k2 + k2 + k	k k1 + 1	k	gcd (A, C) = 1
Denominators of reversed continued fraction	k4	k3	k2	k1	k

Table 5b:  expanded calculation of reverse continued fraction from Table 5a.  The result shows how the numerator of a continued fraction is preserved in its reversal.  It also shows how the denominators are swapped between the continued fraction and its reversal.  

Bézout identity and successive convergents

Calculation of continued fraction truncated at penultimate term (right to left)	a	b	c	1
Calculation of continued fraction (right to left)	d	e	f	g	1
Sub-sequence of continued fraction denominators	kn-3	kn-2	kn-1	kn

Table 6:  illustration of a continued fraction to show how each two-by-two array cross-multiplies to |1|

Consider a simple continued fraction calculated as in Table 6 and presented in an array in the top two rows above.  The bottom row contains the denominators of the continued fraction.  It directs the calculation of the array but is not part of the array under consideration.

First step: Show that the first 2 x 2 array on the right of the table cross-multiplies to |1|.

Second step: Show that if some 2 x 2 array cross-multiplies to |1|, then the next overlapping 2 x 2 array to its left also cross-multiplies to |1|.

We can conclude that all 2 x 2 arrays in the large array cross-multiply to |1|.

This shows that truncating the simple continued fraction at the penultimate term will yield a Bézout identity.  Successive truncations as in Tables 1 and 2 will yield successive convergents to the original continued fraction.  This is because as the continued fraction is successively truncated upwards the resulting sub-arrays will all cross-multiply to |1| and at the final truncation the fraction will be unity. 

 

First step:

By calculation of the array: c = k_n-1 , g = k_n , f = g k_n-1 + 1 = k_n k_n-1 + 1

c.g - f.1 = k_n-1 k_n - (k_n k_n-1 + 1) = -1 = |1|

 

Second step:

Assume that b f - c e = |1|. 

a = b k_n-3 + c

d = e k_n-3 + f

a e - b d = e b k_n-3 +  e c - b e k_n-3 -  b f = ec - bf = |1|

  

In the case of a greatest common divisor greater than 1, it can be shown by a similar argument that each 2 x 2 array will cross-multiply to that greatest common divisor.