Counting fractions

Given a list of fractions, I am looking for a way to identify the nth member of the list without needing to work out all the fractions before the nth one.  Also, given any fraction, I want to be able to say where it appears on the list.

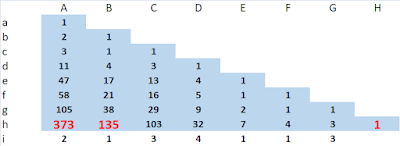
I am looking for reduced fractions, which means that  \( \frac{1}{2} \) will appear in my list but I will not see  \( \frac{2}{4} \), \( \frac{3}{6} \) or any others that can be reduced to simpler terms.

There are methods to create lists of reduced fractions. In particular:
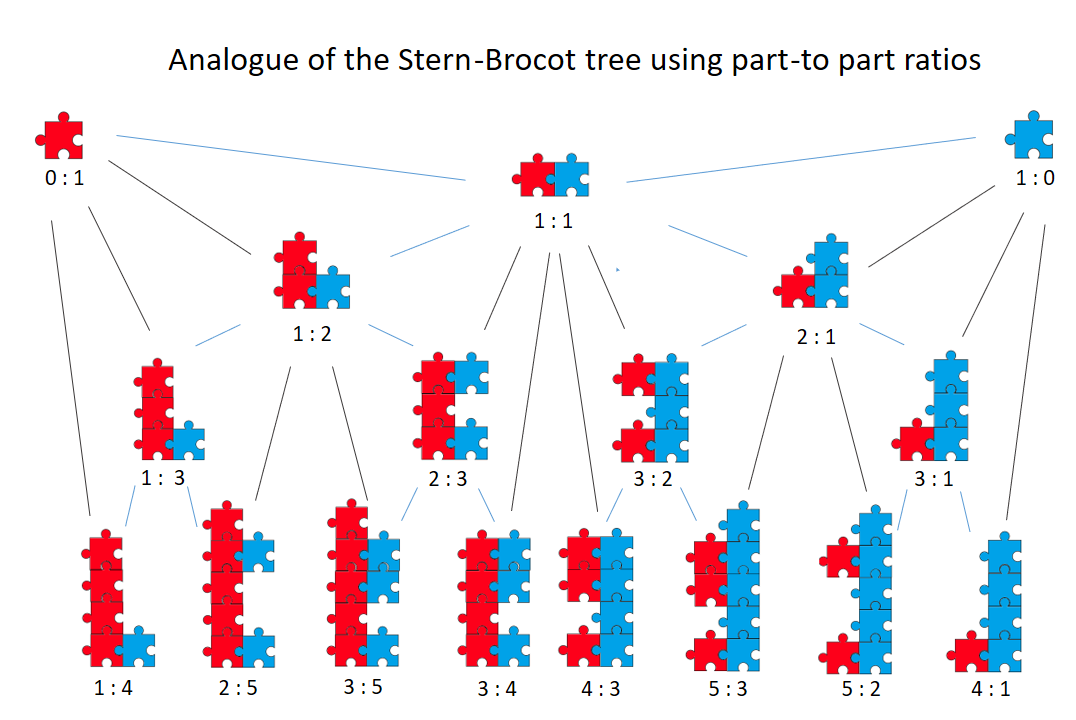
  • The Stern-Brocot tree. 
  • The Calkin Wilf sequence. 
  • Kepler's method in Harmonices Mundi. 
There are methods to locate fractions in these sequences.  Bates, Bunder and Tognetti  presented a method in 2010.  Cut the Knot also discussed binary encoding as a means of locating fractions.  A page on this blog proposes a method that is reasonably simple and intuitive and that yields insight into the structure of fractions.







Comments

Post a Comment

Popular posts from this blog

Continued Fraction Triangle

Image
This post is about patterns in the calculation of a continued fraction and its reverse and in successive  truncations of a continued fraction. Table 1: calculation of continued fraction (row i) from integers 373 and 135 (row h) and calculation of convergents by successively truncating the continued fraction (upwards, rows g to a).  Column H row h is the greatest common divisor of 373 and 135. Table 2:  reverse continued fraction from Table 1 with successive convergents. DESCRIPTION OF TABLES 1 AND 2 Table 1 is a calculation of continued fraction (row i) from integers 373 and 135 (row h) and calculation of convergents by successively truncating the continued fraction by one term at a time (working upwards, rows g to a).  Column H row i is the greatest common divisor of 373 and 135.  The continued fraction can be interpreted as either [2; 1, 3, 4, 1, 1, 3], which represents  \( \frac{373}{135} \) or [0; 2, 1, 3, 4, 1, 1, 3], which is the inverse \( \frac{135}{373} \). Row g of Table 1 ca
Read more

Stern-Brocot Tree and Ratios

Image
  Captions refer to the part-to-part ratio of blue to red units. A jigsaw group of units is made by copying, from the row above it, the two groups between which it will sit (reading left to right) and then by joining them together.   This operation is analogous to calculating the mediant of two fractions by adding numerators and adding denominators. The two u pward lines from each group of units lead to its two ‘parent’ groups and darker lines lead to the more distant of the two parents.  The Stern-Brocot tree generates simple fractions.   The aim is to show that the structure of the Stern-Brocot tree can be reproduced by repeated addition of units without reference to fractions.   In this way the concept ‘one divided by zero’ is obviated in the first row. Achille Brocot was a watch-maker and the Stern-Brocot tree originated in the problem of how to find the best approximations to ideal gear ratios that were too big to manufacture.  Hayes, 2000    In a similar way, the Calkin Wilf tr
Read more