Simply fractions

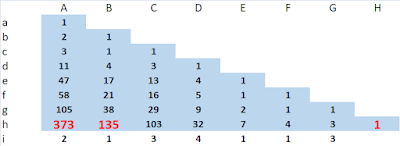
This post is about patterns in the calculation of a continued fraction and its reverse and in successive  truncations of a continued fraction. Table 1: calculation of continued fraction (row i) from integers 373 and 135 (row h) and calculation of convergents by successively truncating the continued fraction (upwards, rows g to a).  Column H row h is the greatest common divisor of 373 and 135. Table 2:  reverse continued fraction from Table 1 with successive convergents. DESCRIPTION OF TABLES 1 AND 2 Table 1 is a calculation of continued fraction (row i) from integers 373 and 135 (row h) and calculation of convergents by successively truncating the continued fraction by one term at a time (working upwards, rows g to a).  Column H row i is the greatest common divisor of 373 and 135.  The continued fraction can be interpreted as either [2; 1, 3, 4, 1, 1, 3], which represents  \( \frac{373}{135} \) or [0; 2, 1, 3, 4, 1, 1, 3], which is the inverse \( \frac{135}{373} \). Row g of Table 1 ca

Given a list of fractions, I am looking for a way to identify the n th member of the list without needing to work out all the fractions before the n th one.  Also, given any fraction, I want to be able to say where it appears on the list. I am looking for reduced fractions, which means that  \( \frac{1}{2} \) will appear in my list but I will not see  \( \frac{2}{4} \), \( \frac{3}{6} \) or any others that can be reduced to simpler terms. There are methods to create lists of reduced fractions. In particular: The Stern-Brocot tree.  The Calkin Wilf sequence.  Kepler's method in Harmonices Mundi.  There are methods to locate fractions in these sequences.  Bates, Bunder and Tognetti   presented a method in 2010.   Cut the Knot also discussed binary encoding as a means of locating fractions.  A page on this blog proposes a method that is reasonably simple and intuitive and that yields insight into the structure of fractions.