Simply fractions

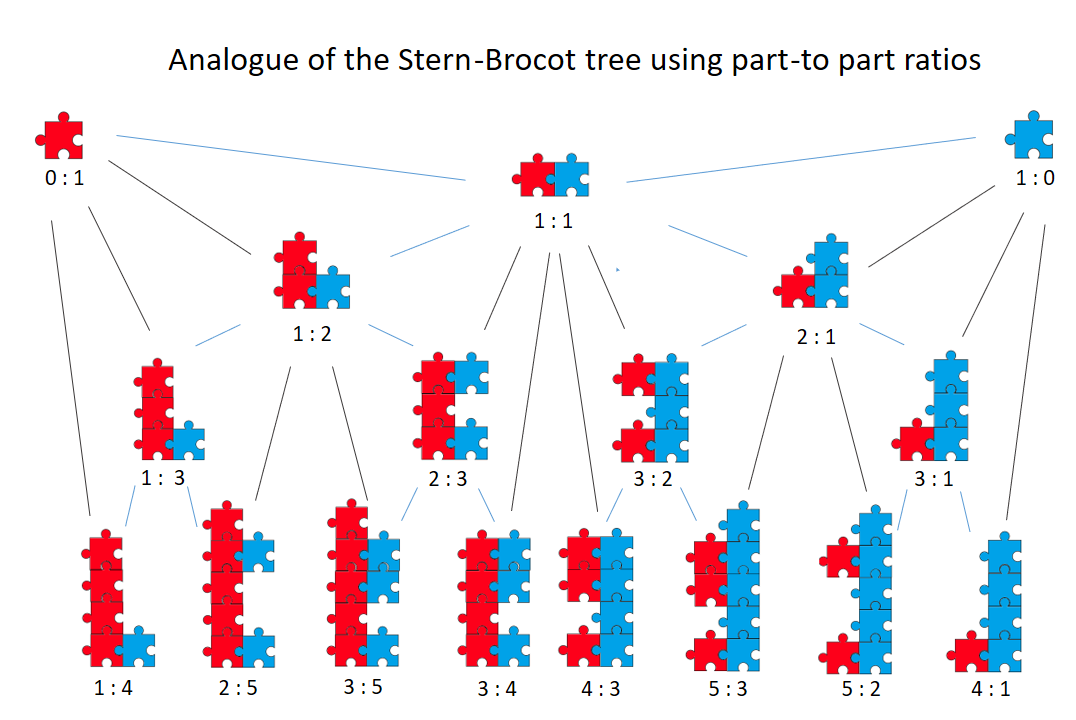
  Captions refer to the part-to-part ratio of blue to red units. A jigsaw group of units is made by copying, from the row above it, the two groups between which it will sit (reading left to right) and then by joining them together.   This operation is analogous to calculating the mediant of two fractions by adding numerators and adding denominators. The two u pward lines from each group of units lead to its two ‘parent’ groups and darker lines lead to the more distant of the two parents.  The Stern-Brocot tree generates simple fractions.   The aim is to show that the structure of the Stern-Brocot tree can be reproduced by repeated addition of units without reference to fractions.   In this way the concept ‘one divided by zero’ is obviated in the first row. Achille Brocot was a watch-maker and the Stern-Brocot tree originated in the problem of how to find the best approximations to ideal gear ratios that were too big to manufacture.  Hayes, 2000    In a similar way, the Calkin Wilf tr